Description

  the design and analysis of a multi degree of freedom (DOF) electro-thermally actuated non-resonant MEMS gyroscope with a 3-DOF drive mode and 1-DOF sense mode system. The 3-DOF drive mode system consists of three masses coupled together using suspension beams. The 1-DOF system consists of a single mass whose motion is decoupled from the drive mode using a decoupling frame. The gyroscope is designed to be operated in the flat region between the first two resonant peaks in drive mode, thus minimizing the effect of environmental and fabrication process variations on device performance. The high gain in the flat operational region is achieved by tuning the suspension beams stiffness. .

  A detailed analytical model, considering the dynamics of both the electro-thermal actuator and multi-mass system, is developed. A parametric optimization is carried out, considering the microfabrication process constraints of the Metal Multi-User MEMS Processes (MetalMUMPs), to achieve high gain. The stiffness of suspension beams is optimized such that the sense mode resonant frequency lies in the flat region between the first two resonant peaks in the drive mode. The results acquired through the developed analytical model are verified with the help of 3D finite element method (FEM)-based simulations. The first three resonant frequencies in the drive mode are designed to be 2.51 kHz, 3.68 kHz, and 5.77 kHz, respectively. The sense mode resonant frequency is designed to be 3.13 kHz. At an actuation voltage of 0.2 V, the dynamically amplified drive mode gain in the sense mass is obtained to be 18.6 µm. With this gain, a capacitive change of 28.11 f F and 862.13 f F is achieved corresponding to the sense mode amplitude of 0.15 µm and 4.5 µm at atmospheric air pressure and in a vacuum, respectively.

Operating Principle

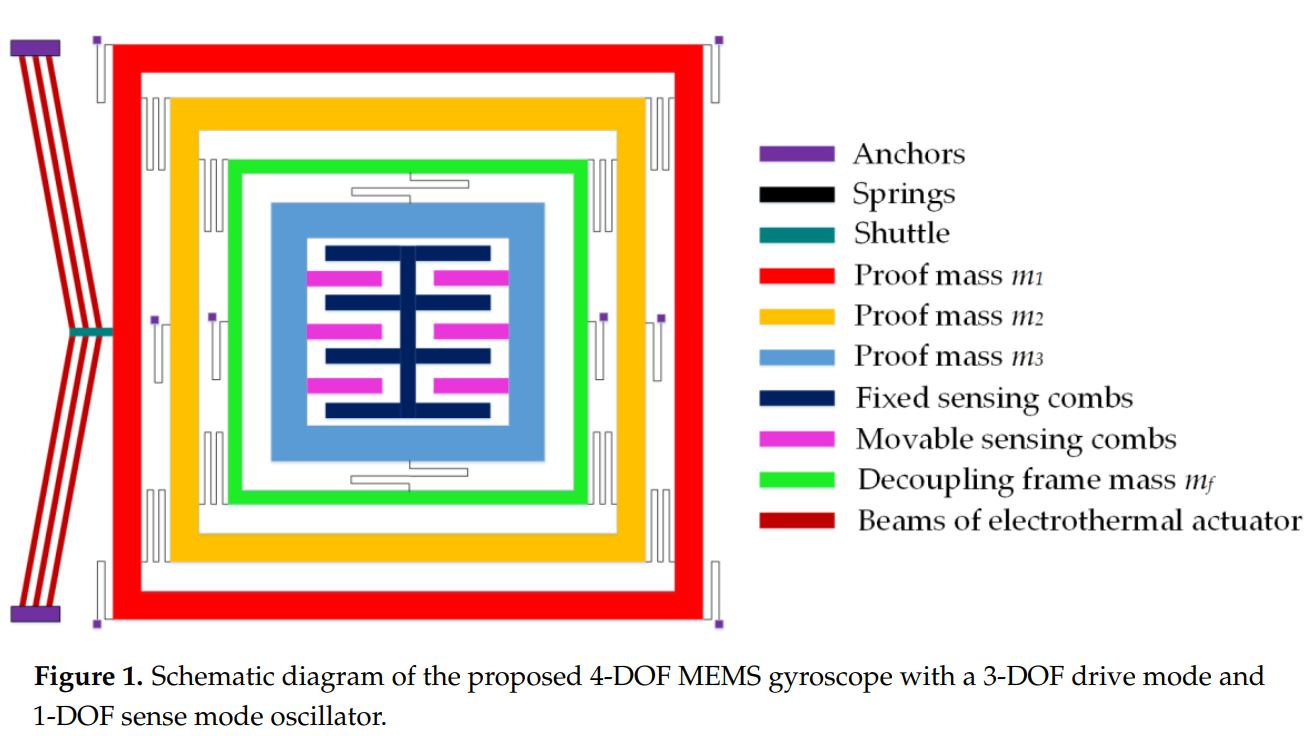
  Figure 1 shows the schematic of the proposed MEMS gyroscope with a 3-DOF drive mode and 1-DOF sense mode. The first mass m1 which is the drive mass is excited by an external force in the drive direction using the V-shaped electro thermal actuator. The second mass m2 transfers the dynamic energy from the mass m1 to mass m3 which acts as a final oscillating mass. The masses m1 and m2 are free to move in the drive direction but constrained to move in the sense direction by means of elastic springs. The sense mode oscillations of mass m3 are decoupled from the drive direction oscillations by means of a decoupling frame mf to minimize instabilities due to dynamical coupling between sense and drive modes. Thus, masses m1, m2, and combination of (mf + m3) form a 3-DOF drive mode while m3 being free to oscillate in the sense acts as a 1-DOF sense mode oscillator. The sense direction oscillation of the mass m3, corresponding to an input angular velocity, is designed to be measured by using parallel plate sense combs.

Analytical Modeling

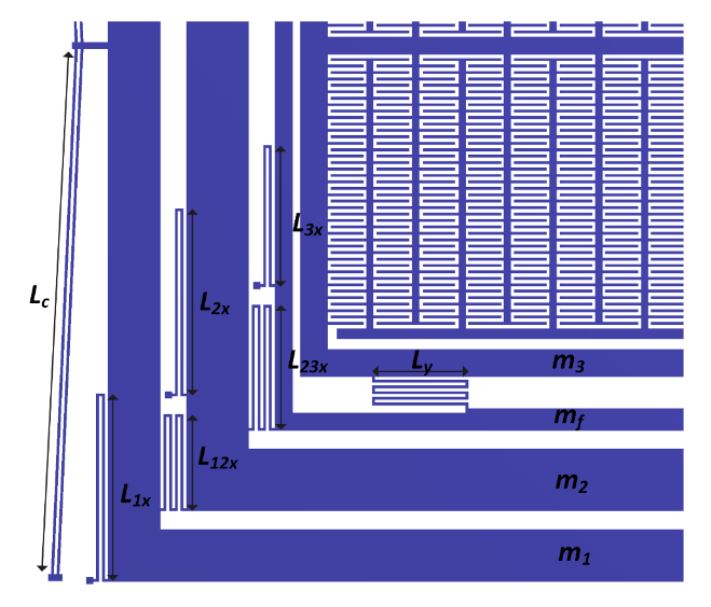
   The designed suspension system configuration of the proposed gyroscope allows the masses m1 and m2 to move only in the drive direction but restricted their motion in the sense direction. The mass m3 is allowed to oscillate in both the drive and sense direction which are orthogonal to each other. The suspension system configuration of the proposed gyroscope dynamical model is shown in Figure below.

FEM Analysis

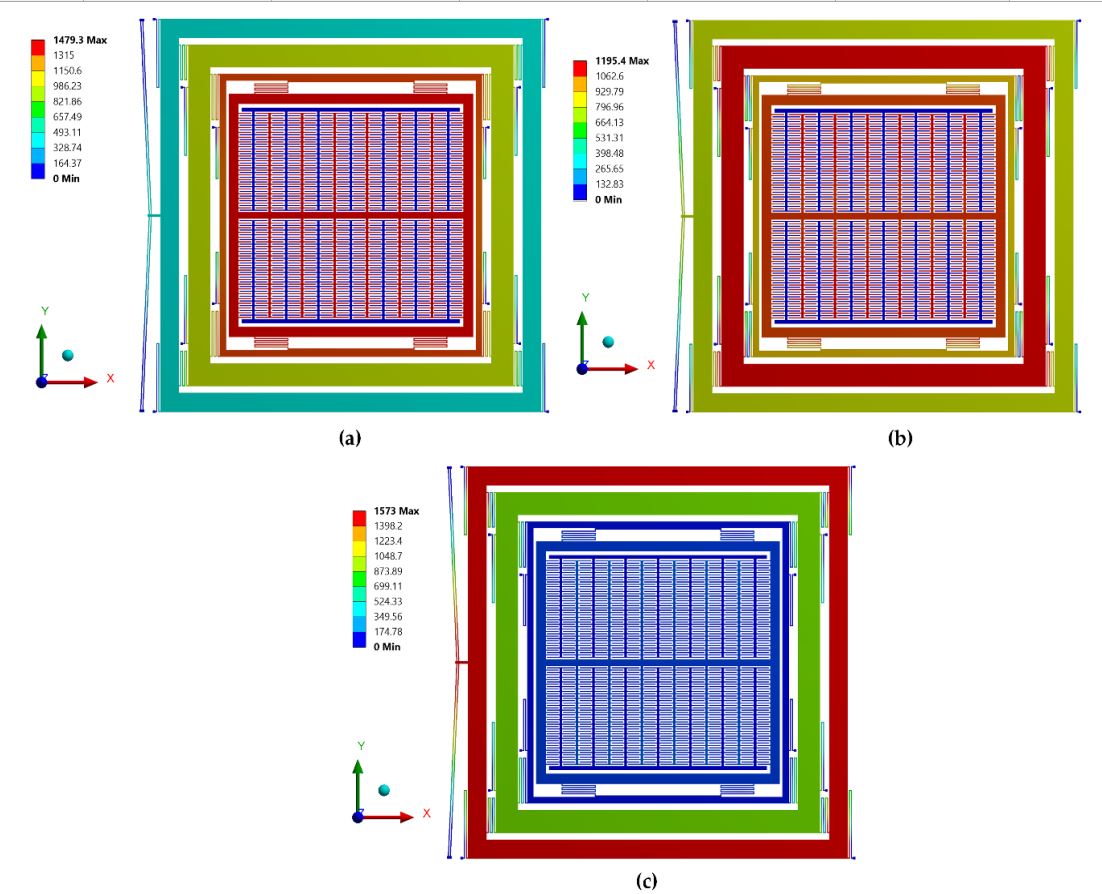
   a FEM-based natural frequency analysis is carried out. The boundary conditions and material properties are input parameters while mode shapes and resonant frequencies are the output responses of the modal analysis. The structural parts are modeled using Solid 98 elements. The optimized mesh size is selected based on patch conforming algorithm for tetrahedrons method control. The desired mode shapes with their associated resonant frequencies are shown in Figure 14. Table 3 shows the comparison of the drive mode resonant frequencies obtained using FEM analysis to that obtained using an analytical model. The percentage deviation is less than 1%, thus validating the accuracy of the developed analytical model.

Matlab Code

   For MATLAB code, please click the Link-1

CAD Model

   For CAD Model, please click the Link-2